Matlab: Control theory (transfer_function, bode,rootlocus

Here is a simple Matlab code for control theory like bode plot, root locus, and transfer function. You could either use symbolic method, which using 's' as Laplace symbol or directly key in into vector form (easier).




------------------------------------------------------------------------------------------
clc
clear

syms s %construct symbolic object


F1=20*(s+3)*(s+7)/[(s+5)*(s+2)^2];
display('F1(s)=')
pretty(F1)

F2=1/[s^2+8*s+16]
display('F2(s)=')
pretty(F2)

F3=F1*F2;
display('F3(s)=F1(s)*F2(s)=')
pretty(F3)

f=ilaplace(F3);
display('Inverse Laplace for F3(s):')
pretty(f)


[num,den]=numden(F3); %extract symbolic numerator and denominator
num=sym2poly(num); %form vector for numerator
den=sym2poly(den); %form vector for denominator

Gtf=tf(num,den) %G(s) in polynomial form
Gzpk=zpk(Gtf) %convert G(s) to factored form

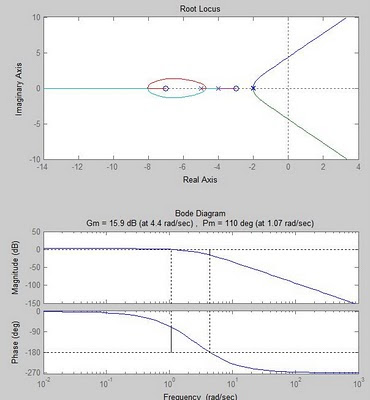
subplot(2,1,1)
rlocus(Gzpk) %root locus plot
%sgrid %turn on grid for damping ratio

subplot(2,1,2)
%bode(Gzpk) %bode plot
margin(Gzpk) %find and plot phase & gain margin

-----------------------Result----------------------------------------
F1(s)=

(20 s + 60) (s + 7)
-------------------
2
(s + 5) (s + 2)

F2(s)=

1
-------------
2
s + 8 s + 16

F3(s)=F1(s)*F2(s)=

(20 s + 60) (s + 7)
--------------------------------
2 2
(s + 5) (s + 2) (s + 8 s + 16)

Inverse Laplace for F3(s):

- 80/9 exp(-5 t) + (25/3 t - 10/9) exp(-2 t) + (-15 t + 10) exp(-4 t)

Transfer function:
20 s^2 + 200 s + 420
----------------------------------------------
s^5 + 17 s^4 + 112 s^3 + 356 s^2 + 544 s + 320


Zero/pole/gain:
20 (s+7) (s+3)
---------------------
(s+5) (s+4)^2 (s+2)^2

%%%%%%%%%%%%%%%%%

the red color indicates display problem when posting them in html (displacement)
%%%%%%%%%%%%%%%%%%

-----------------------------------------------------------------------------
Here is the Matlab code for bode plot. It plots out both open loop & close loop response for comparison.

clc
clf
clear
num=1.61e12*poly( -1.37e6);
den=poly([0 0 -2.6e6]);
'G(s)'
G=tf(num,den) %open loop
T=feedback(G,1); %negative feedback 1 (close loop)


subplot(2,1,1)
margin(G)
%grid on

subplot(2,1,2)
margin(T)
%grid on

figure %create new figure
margin(G)
hold on %allow overlap
margin(T)
%grid on